Training an MLP (CPU and GPU)#
In this notebook, we’ll train a simple Multi-Layer Perceptron (MLP) to learn a sine wave function. The primary goal is to demonstrate and compare Nabla’s different execution modes, showcasing how Just-In-Time (JIT) compilation can dramatically accelerate model training.
Note: To create a heavy computational workload and clearly demonstrate performance gains, the MLP used here is intentionally oversized. A much smaller network would be sufficient and probably better for this task, but the larger model allows us to stress-test the JIT compiler and clearly see the speedup from hardware acceleration.
1. Imports and Setup#
First, we’ll import the necessary libraries: nabla for deep learning, numpy, matplotlib for plotting, and time for benchmarking.
[1]:
import sys
import time
from typing import Any, Callable, List
try:
import matplotlib.pyplot as plt
import numpy as np
import nabla as nb
except ImportError:
import subprocess
packages = ["numpy", "nabla-ml", "matplotlib"]
subprocess.run([sys.executable, "-m", "pip", "install"] + packages, check=True)
import matplotlib.pyplot as plt
import numpy as np
import nabla as nb
print(
f"🎉 All libraries loaded successfully! Python {sys.version_info.major}.{sys.version_info.minor}"
)
🎉 All libraries loaded successfully! Python 3.10
2. Configuration#
Here we define the key hyperparameters for our model architecture and the training process.
[2]:
# Model & Task Configuration
LAYERS = [1, 256, 1024, 2048, 2048, 1024, 256, 1] # Defines the architecture of our MLP
SIN_PERIODS = 8 # The complexity of the sine wave we want to learn
# Training Configuration
BATCH_SIZE = 512
LEARNING_RATE = 0.001 # Using a constant learning rate
NUM_EPOCHS = 500
PRINT_INTERVAL = 100
3. Model and Loss Function#
mlp_forward: Defines the forward pass of our MLP.mean_squared_error: Our loss function.
[3]:
def mlp_forward(x: nb.Array, params: list[nb.Array]) -> nb.Array:
"""MLP forward pass through all layers."""
output = x
for i in range(0, len(params) - 1, 2):
w, b = params[i], params[i + 1]
output = nb.matmul(output, w) + b
if i < len(params) - 2:
output = nb.relu(output)
return output
def mean_squared_error(predictions: nb.Array, targets: nb.Array) -> nb.Array:
"""Compute mean squared error loss."""
diff = predictions - targets
squared_errors = diff * diff
batch_size = nb.array(predictions.shape[0], dtype=nb.DType.float32)
loss = nb.sum(squared_errors) / batch_size
return loss
4. Data Generation and Parameter Initialization#
create_sin_dataset: Generates a batch of training data.initialize_mlp_params: Creates and initializes the model’s parameters.
[4]:
def create_sin_dataset(batch_size: int) -> tuple[nb.Array, nb.Array]:
"""Create a batch of data for the n-period sine function."""
x_np = np.random.rand(batch_size, 1).astype(np.float32)
targets_np = (np.sin(SIN_PERIODS * 2.0 * np.pi * x_np) / 2.0 + 0.5).astype(
np.float32
)
return nb.Array.from_numpy(x_np), nb.Array.from_numpy(targets_np)
def initialize_mlp_params(layers: list[int], seed: int = 42) -> list[nb.Array]:
"""Initialize MLP parameters using He normal initialization."""
params = []
for i in range(len(layers) - 1):
w = nb.he_normal((layers[i], layers[i + 1]), seed=seed)
b = nb.zeros((layers[i + 1],))
params.append(w)
params.append(b)
return params
5. Optimizer (AdamW)#
This is the original, simple implementation of the AdamW optimizer, without gradient clipping.
[5]:
def init_adamw_state(
params: list[nb.Array],
) -> tuple[list[nb.Array], list[nb.Array]]:
"""
Initializes the momentum (m) and variance (v) states for the AdamW optimizer.
Each state is initialized as a zero-tensor with the same shape as its
corresponding parameter.
"""
m_states = [nb.zeros(p.shape) for p in params]
v_states = [nb.zeros(p.shape) for p in params]
return m_states, v_states
def adamw_step(
params: list[nb.Array],
gradients: list[nb.Array],
m_states: list[nb.Array],
v_states: list[nb.Array],
step: int,
learning_rate: float,
beta1: float = 0.9,
beta2: float = 0.999,
eps: float = 1e-8,
weight_decay: float = 0.01,
max_grad_norm: float = 1.0,
) -> tuple[list[nb.Array], list[nb.Array], list[nb.Array]]:
"""
Performs a single step of the AdamW optimizer with a robust gradient clipping implementation.
"""
# --- Corrected Gradient Clipping (mirroring the Transformer logic) ---
# 1. Calculate the total norm.
total_norm_sq = sum(nb.sum(g * g) for g in gradients)
total_norm = nb.sqrt(total_norm_sq)
# 2. Use nb.minimum to get a single, simple scaling factor. This is the key change.
clip_factor = nb.minimum(1.0, max_grad_norm / (total_norm + 1e-8))
# 3. Apply the single factor to all gradients. This creates a much simpler graph.
clipped_gradients = [g * clip_factor for g in gradients]
# --- Standard AdamW Update Logic ---
updated_params = []
updated_m = []
updated_v = []
for param, grad, m, v in zip(params, clipped_gradients, m_states, v_states):
new_m = beta1 * m + (1.0 - beta1) * grad
new_v = beta2 * v + (1.0 - beta2) * (grad * grad)
m_corr = new_m / (1.0 - beta1**step)
v_corr = new_v / (1.0 - beta2**step)
new_param = param - learning_rate * (
m_corr / (nb.sqrt(v_corr) + eps) + weight_decay * param
)
updated_params.append(new_param)
updated_m.append(new_m)
updated_v.append(new_v)
return updated_params, updated_m, updated_v
6. Defining the Core Training Step#
This function encapsulates a single training step. We are using the original, working value_and_grad pattern that takes a variable number of arguments, which is known to be correct for this simpler setup.
[6]:
def _complete_training_step(
x: nb.Array,
targets: nb.Array,
params: list[nb.Array],
m_states: list[nb.Array],
v_states: list[nb.Array],
step: int,
) -> tuple[list[nb.Array], list[nb.Array], list[nb.Array], nb.Array]:
"""The core, undecorated logic for a single training step."""
def loss_fn(*inner_params):
predictions = mlp_forward(x, list(inner_params))
return mean_squared_error(predictions, targets)
loss_value, param_gradients = nb.value_and_grad(
loss_fn, argnums=list(range(len(params)))
)(*params)
updated_params, updated_m, updated_v = adamw_step(
params, param_gradients, m_states, v_states, step, LEARNING_RATE
)
return updated_params, updated_m, updated_v, loss_value
7. Defining the Execution Modes#
Now we create our three different training functions to compare performance.
[7]:
# Mode 1: Eager step (just an alias to the original function)
eager_training_step = _complete_training_step
# Mode 2: JIT-compiled step for CPU execution
jit_cpu_training_step = nb.jit(_complete_training_step, auto_device=False)
# Mode 3: (Optional) JIT-compiled step with automatic device placement
if nb.accelerator_count() > 0:
jit_accelerator_training_step = nb.jit(_complete_training_step, auto_device=True)
print(f"✅ Accelerator detected! '{nb.accelerator()}' will be used for the third run.")
else:
jit_accelerator_training_step = None
print("INFO: No accelerator detected. The accelerator-based training run will be skipped.")
✅ Accelerator detected! 'Device(type=gpu,id=0)' will be used for the third run.
8. Training and Benchmarking Loop#
This generic run_training_loop function executes the training process for a given step function, handling initialization, the main loop, and timing.
[8]:
def run_training_loop(
mode_name: str, training_step_fn: Callable[..., Any]
) -> dict[str, Any]:
"""Generic training loop to benchmark a given training step function."""
print("=" * 60)
print(f"🤖 TRAINING MLP IN {mode_name.upper()} MODE")
print("=" * 60)
params = initialize_mlp_params(LAYERS)
m_states, v_states = init_adamw_state(params)
print("🔥 Warming up (3 steps)...")
for i in range(3):
x, targets = create_sin_dataset(BATCH_SIZE)
params, m_states, v_states, _ = training_step_fn(
x, targets, params, m_states, v_states, i + 1
)
print("✅ Warmup complete! Starting timed training...\n")
start_time = time.time()
loss_history = []
time_history = [start_time]
for epoch in range(1, NUM_EPOCHS + 1):
x, targets = create_sin_dataset(BATCH_SIZE)
params, m_states, v_states, loss = training_step_fn(
x, targets, params, m_states, v_states, epoch
)
loss_history.append(float(loss.to_numpy()))
time_history.append(time.time())
if epoch % PRINT_INTERVAL == 0:
avg_loss = np.mean(loss_history[-PRINT_INTERVAL:])
print(f"Epoch {epoch:5d} | Avg Loss: {avg_loss:.6f} | Time: {time_history[-1] - start_time}")
total_time = time_history[-1] - start_time
print(f"\n✅ {mode_name} Training complete! Total time: {total_time:.2f}s")
return {
"params": params,
"loss_history": loss_history,
"time_history": time_history,
"total_time": total_time,
}
# --- Run all training modes ---
results = {}
results["Eager"] = run_training_loop("Eager", eager_training_step)
results["JIT (CPU)"] = run_training_loop("JIT (CPU)", jit_cpu_training_step)
if jit_accelerator_training_step:
results["JIT (Accelerator)"] = run_training_loop(
"JIT (Accelerator)", jit_accelerator_training_step
)
============================================================
🤖 TRAINING MLP IN EAGER MODE
============================================================
🔥 Warming up (3 steps)...
✅ Warmup complete! Starting timed training...
Epoch 100 | Avg Loss: 1.960438 | Time: 21.644721269607544
Epoch 200 | Avg Loss: 0.101309 | Time: 42.536442279815674
Epoch 300 | Avg Loss: 0.092507 | Time: 63.919116258621216
Epoch 400 | Avg Loss: 0.083474 | Time: 84.2975525856018
Epoch 500 | Avg Loss: 0.085233 | Time: 105.92598056793213
✅ Eager Training complete! Total time: 105.93s
============================================================
🤖 TRAINING MLP IN JIT (CPU) MODE
============================================================
🔥 Warming up (3 steps)...
✅ Warmup complete! Starting timed training...
Epoch 100 | Avg Loss: 1.970259 | Time: 4.292894124984741
Epoch 200 | Avg Loss: 0.100773 | Time: 8.325119733810425
Epoch 300 | Avg Loss: 0.090923 | Time: 12.33992314338684
Epoch 400 | Avg Loss: 0.086043 | Time: 16.240766763687134
Epoch 500 | Avg Loss: 0.083217 | Time: 20.310790538787842
✅ JIT (CPU) Training complete! Total time: 20.31s
============================================================
🤖 TRAINING MLP IN JIT (ACCELERATOR) MODE
============================================================
🔥 Warming up (3 steps)...
✅ Warmup complete! Starting timed training...
Epoch 100 | Avg Loss: 1.780899 | Time: 0.30668044090270996
Epoch 200 | Avg Loss: 0.100820 | Time: 0.5730481147766113
Epoch 300 | Avg Loss: 0.090581 | Time: 0.8387882709503174
Epoch 400 | Avg Loss: 0.084966 | Time: 1.1043381690979004
Epoch 500 | Avg Loss: 0.083767 | Time: 1.3704478740692139
✅ JIT (Accelerator) Training complete! Total time: 1.37s
9. Performance Comparison#
Let’s visualize the results. The ‘Loss vs. Time’ plot remains the best way to see the raw speed advantage of JIT compilation.
[9]:
def plot_performance_comparison(results: dict[str, Any]):
"""Plot the loss curves for all completed training runs."""
if not results:
print("No results to plot.")
return
plt.figure(figsize=(16, 7))
# Plot loss vs epochs
plt.subplot(1, 2, 1)
for mode, data in results.items():
plt.plot(data["loss_history"], label=f'{mode} (Total: {data["total_time"]:.2f}s)')
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Loss vs. Epochs")
plt.yscale("log")
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
# Plot loss vs time
plt.subplot(1, 2, 2)
for mode, data in results.items():
relative_times = [t - data["time_history"][0] for t in data["time_history"]]
plt.plot(relative_times[1:], data["loss_history"], label=mode)
if 'JIT (CPU)' in results:
xlim_max = results['JIT (CPU)']['total_time'] * 1.05
plt.xlim(0, xlim_max)
plt.xlabel("Time (seconds)")
plt.ylabel("Loss")
plt.title("Loss vs. Time (Zoomed In)")
plt.yscale("log")
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.tight_layout()
plt.show()
plot_performance_comparison(results)
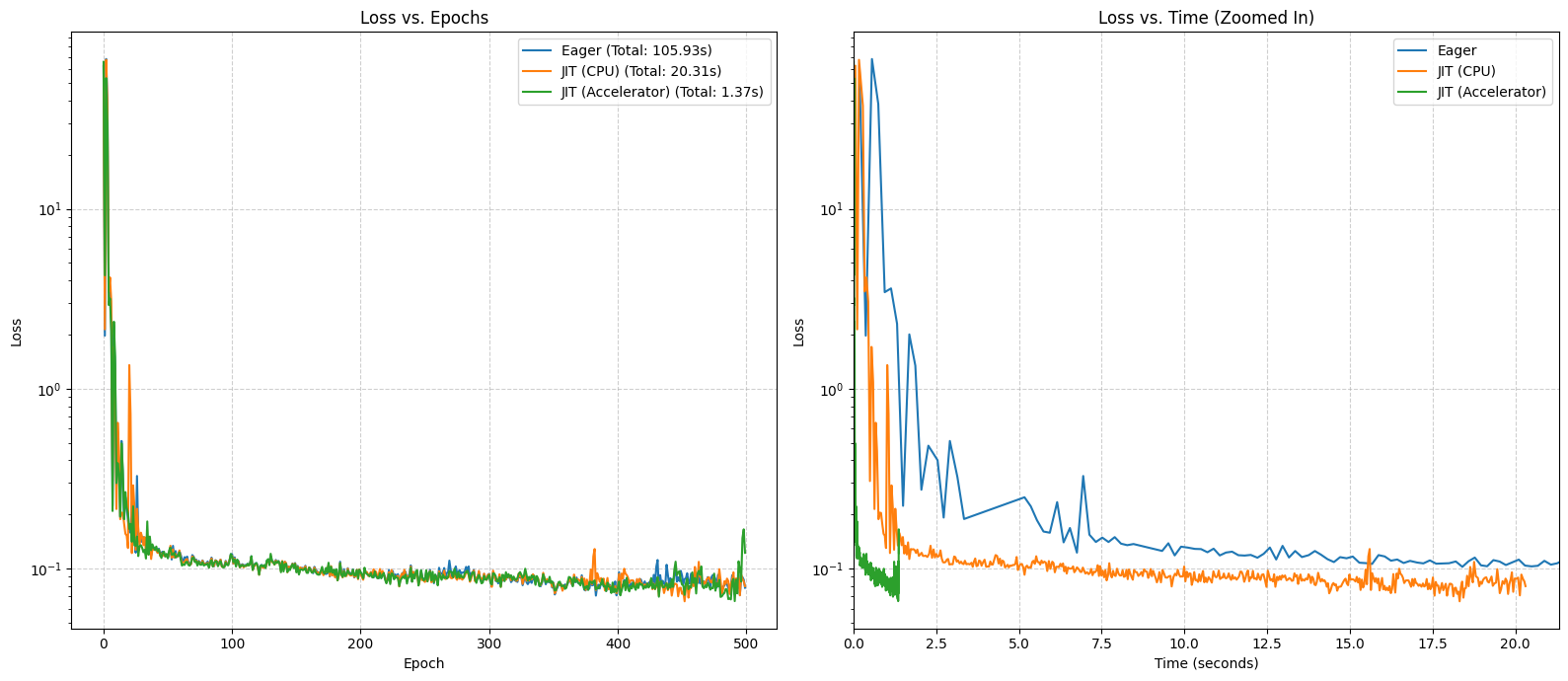
10. Final Evaluation & Visualization#
Finally, we take the model from the fastest training run and see how well it learned the sine wave. We plot its predictions against the true function for a clear visual evaluation.
[10]:
def evaluate_and_plot_model(params: List[nb.Array]):
"""Evaluates the final model and plots its predictions against the ground truth."""
print("\n" + "=" * 60)
print("🧪 FINAL MODEL EVALUATION")
print("=" * 60)
# Create a high-resolution test set for a smooth plot
x_test_np = np.linspace(0, 1, 1000).reshape(-1, 1).astype(np.float32)
targets_test_np = (np.sin(SIN_PERIODS * 2.0 * np.pi * x_test_np) / 2.0 + 0.5).astype(
np.float32
)
x_test = nb.Array.from_numpy(x_test_np)
# Get predictions from the model
predictions_test = mlp_forward(x_test, params)
pred_final_np = predictions_test.to_numpy()
# Calculate final loss and correlation
final_loss = np.mean((pred_final_np - targets_test_np) ** 2)
correlation = np.corrcoef(pred_final_np.flatten(), targets_test_np.flatten())[0, 1]
print(f"Final Test Loss: {final_loss:.6f}")
print(f"Prediction-Target Correlation: {correlation:.4f}")
# Plot the results
plt.figure(figsize=(12, 6))
plt.plot(x_test_np, targets_test_np, label='Ground Truth', color='blue', linestyle='--')
plt.plot(x_test_np, pred_final_np, label='Model Prediction', color='red', alpha=0.8)
plt.title('Final Model Prediction vs. Ground Truth')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()
# Find the best parameters from the fastest run and evaluate
if results:
fastest_mode = min(results, key=lambda mode: results[mode]["total_time"])
print(f"\nEvaluating model from the fastest run: '{fastest_mode}'")
best_params = results[fastest_mode]['params']
evaluate_and_plot_model(best_params)
else:
print("\nSkipping evaluation as no training runs were completed.")
Evaluating model from the fastest run: 'JIT (Accelerator)'
============================================================
🧪 FINAL MODEL EVALUATION
============================================================
Final Test Loss: 0.100042
Prediction-Target Correlation: 0.4524
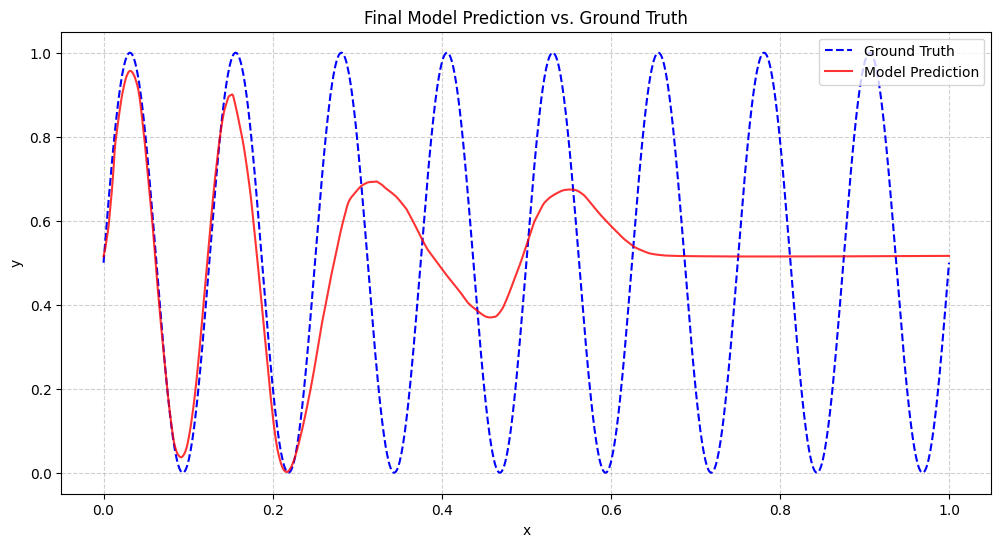
11. Conclusion#
This experiment successfully demonstrates a key principle: for large computational workloads, hardware acceleration is a necessity. Although the training dynamics were unstable, the performance results are unambiguous. The nearly 15x speedup is a powerful illustration of how accelerators make training large models feasible in practice.